Modellbasierter Entwurf optimaler Reaktoren

Forschende: Elodia Morales, Mathias Waldner

Ein Forschungsschwerpunkt des Lehrstuhls „Reaction Engineering and Catalysis“ liegt auf der Entwicklung optimaler katalytischer Reaktoren zur Realisierung hocheffizienter chemischer Prozesse. Ziel der Optimierung ist es, eine möglichst hohe Ausbeute des gewünschten Produktes zu erreichen und gleichzeitig den Energie- und Ressourcenbedarf zu minimieren. Um dies zu erreichen, wird auf das in unserer Gruppe entwickelte Konzept des Multi-Level Reactor Designs (MLRD) zurückgegriffen. Dieses lässt sich in vier Level unterteilen.

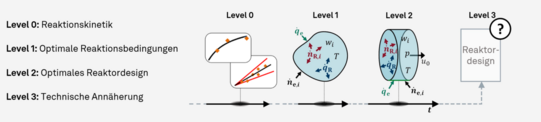
Voraussetzung für den modellbasierten Reaktorentwurf mittels MLRD ist die Beschreibung der ablaufenden Reaktionen durch ein reaktionskinetisches Modell. Da dies ein ganz entscheidender erster Schritt ist, ist dieser Thematik ein eigener Forschungsbereich (Reaktionskinetik: Experimente, Netzwerkanalyse und Modellierung) gewidmet. Ist ein Modell mit adäquatem Detailgrad zur Beschreibung des realen Reaktionsnetzwerkes aufgestellt, wird mit der Ermittlung und detaillierten Betrachtung des idealen Reaktionspfades begonnen (Level 1).

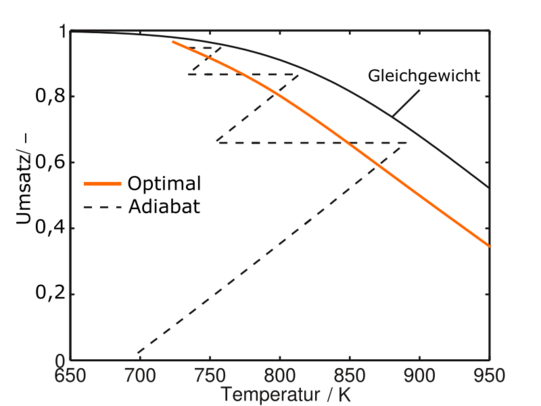
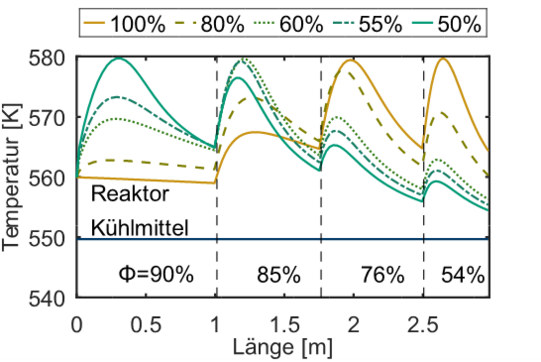
Zur besseren Verständlichkeit soll das MLRD-Konzept exemplarisch an einem einfachen konkreten Beispiel, der Oxidation von Schwefeldioxid (SO₂) zu Schwefeltrioxid (SO₃), vorgestellt werden. Diese Reaktion ist ein entscheidender Schritt in der Herstellung von Schwefelsäure nach dem Doppelkontaktverfahren. Auf Level 1 wird der ideale Reaktionspfad bis zu einem gewünschten Umsatz betrachtet. Ziel ist es dabei, die hierfür benötigte Reaktionszeit zu minimieren, daher wird eine möglichst hohe Reaktionsrate angestrebt. Nach Arrhenius ist hierfür eine hohe Temperatur erforderlich. Da es sich bei der Oxidation von SO₂ jedoch um eine exotherme Gleichgewichtsreaktion handelt, darf die Temperatur nicht zu hoch gewählt werden, um Limitierungen durch eine ungünstige Gleichgewichtslage zu vermeiden. Somit existiert eine optimale Temperatur, bei welcher die Reaktion durchgeführt werden sollte. Dieser optimale Reaktionspfad ist im folgenden Diagramm dargestellt.

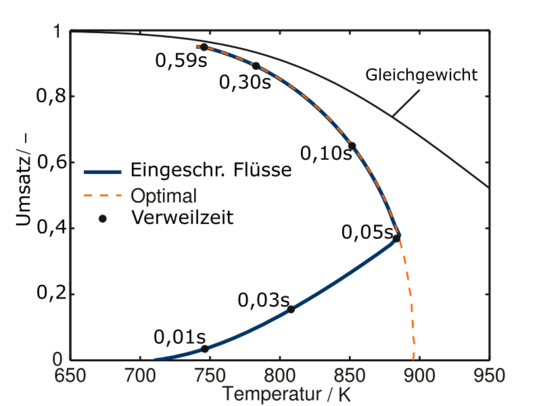
Zusätzlich zum idealen Reaktionspfad ist im Diagramm für Level 1 der aktuelle Stand der Technik im adiabaten Hordenreaktor dargestellt. Die Ermittlung des optimalen Reaktionspfades erfolgt unter Annahme von uneingeschränktem Wärme- und Stofftransport im Reaktor. In der Realität treten jedoch besonders bei hohen Temperaturen Stofftransportlimitierungen auf, welche auf Level 2 der MLRD Methodik berücksichtigt wer­den. An dieser Stelle werden auch bereits erste idealisierte Reaktorkonzepte in die Betrachtung mit einbezogen. Der resultierende Reaktionspfad weicht bei hohen Temperaturen und geringen Umsätzen stark vom optimalen Reaktionspfad ab.

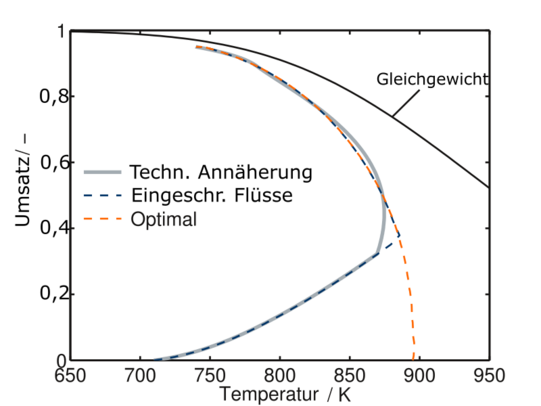
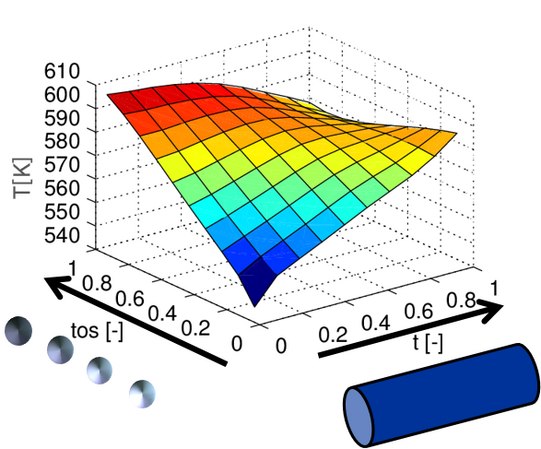
Im letzten Schritt (Level 3) wird die technische Umsetzbarkeit des erarbeiteten optimalen Reaktorkonzepts ermittelt. Hierbei spielen die in der Realität durch die technischen Gegebenheiten nur endlich schnell ablaufenden Wärme- und Stofftransportvorgänge im Reaktor sowie eine optimierte Temperaturführung eine entscheidende Rolle. An dieser Stelle werden verschiedene Betriebskonzepte betrachtet und die technisch mögliche Regelungstechnik berücksichtigt. Das Ergebnis ist die im Rahmen der technischen Möglichkeiten optimale Reaktionsführung.

Das hier vorgestellte einfache Beispiel dient lediglich zur anschaulichen Erklärung. Die MLRD Methodik wurde über die letzten Jahre um viele substantielle Aspekte und Anwendungsmöglichkeiten erweitert. So ist MLRD ebenso anwendbar für hochkomplexe Reaktionsnetzwerke mit bis zu ca. 70 Reaktionen. Gerade für solch komplexen Systeme ist die optimale Lösung häufig stark nichtintuitiv und nicht mehr durch Heuristiken vorhersagbar.
 

Zu­dem kann die Op­ti­mie­rung ebenso mit zweidimensionalen Reaktormodellen durch­ge­führt wer­den, sofern dies auf­grund starker radialer Gradienten er­for­der­lich oder zum besseren Ver­ständ­nis der Er­geb­nisse not­wen­dig ist. Ebenfalls wurde bereits eine Lebenszyklusoptimierung durch­ge­führt, indem die Op­ti­mie­rung die ge­sam­te Standzeit eines mit der Zeit desaktivierenden Katalysators be­rück­sich­tigt. Dieser Ansatz kann umgekehrt auch zur Op­ti­mie­rung der Standzeit des Katalysators und zum Vergleich ver­schie­dener Katalysatoren über die Standzeit ver­wen­det wer­den.

Weitere erfolgreiche Anwendungen der MLRD Methodik umfassen die Optimierung von dynamisch betriebenen Reaktoren, die Optimierung unter Unsicherheiten, die Mehrzieloptimierung, die Berücksichtigung rigoroser Diffusionsmodelle sowie in diesem Hinblick auch verallgemeinert die Berücksichtigung des Katalysatorpellets für das integrierte optimale Design des Gesamtsystems Katalysator-Reaktor.

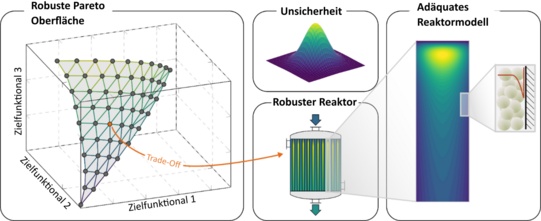
Eine zusätzliche Erweiterung stellt die Behandlung von Mehrphasensystemen dar. Der einfachere Fall eines schnellen Stoffübergangs zwischen den Phasen kann dabei in Analogie zum einphasigen Fall (die zweite Phase dient lediglich als Reservoir) betrachtet werden. Liegen dagegen Stofftransportlimitierungen im System vor, so müssen beide Phasen in der Modellierung explizit berücksichtigt werden. In diesem Zusammenhang wurde die Anwendbarkeit und das Potential der MLRD Methodik für die Optimierung von reaktiven Trennapparaten am Beispiel der Optimierung eines chemischen Absorbers eindrucksvoll unter Beweis gestellt.